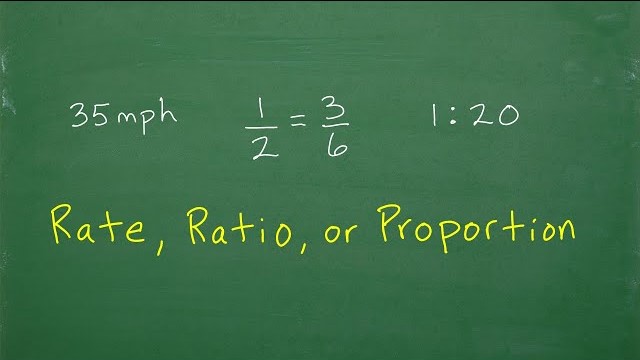📘 About Ratio, Proportion, and Rates
Ratio is used to compare quantities of the same kind, showing how much of one thing there is compared to another.
-
Example: A juice mix might have a ratio of 2:5 (2 parts concentrate to 5 parts water).
-
Ratios can be simplified just like fractions.
Proportion refers to the equality of two ratios and helps solve problems involving scaling or balancing quantities.
-
Example: If 3 pencils cost $1.50, how much do 9 pencils cost? Set up the proportion:
31.50=9x\frac{3}{1.50} = \frac{9}{x} and solve for xx.
Rates involve two different types of quantities and often use the word "per" (e.g., speed, price, density).
-
Example: A car travels at 60 km per hour, or apples cost $3 per kg.
📊 Skills Developed
-
Comparing and scaling numbers accurately.
-
Applying mathematical reasoning to real-life problems like recipes, map reading, and budgeting.
-
Preparing for advanced topics like algebra, percentages, and data analysis.
🧠 Example Topics
-
Simplifying ratios: 10:20=1:210:20 = 1:2
-
Using ratio in recipes: Doubling or halving quantities using the given ratio.
-
Solving proportions: Cross-multiplication to find missing values.
-
Calculating rates: Speed=DistanceTime\text{Speed} = \frac{\text{Distance}}{\text{Time}}
-
Unit pricing: Comparing costs to find the best deal (e.g., $/100g vs. $/1kg)
- Evening Class
- Mathematics
- 1
- 3 hours
- Members